606. Construct String from Binary Tree

Problem Description

Given the root of a binary tree, construct a string consisting of parenthesis and integers from a binary tree with the preorder traversal way, and return it.

Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.

Example 1:

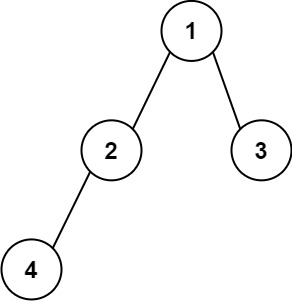
Input: root = [1,2,3,4]
Output: "1(2(4))(3)"
Explanation: Originally, it needs to be "1(2(4)())(3()())", but you need to omit all the unnecessary empty parenthesis pairs. And it will be "1(2(4))(3)"

Example 2:

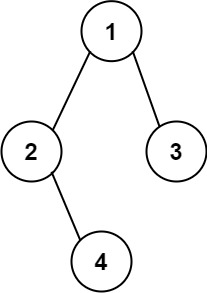
Input: root = [1,2,3,null,4]
Output: "1(2()(4))(3)"
Explanation: Almost the same as the first example, except we cannot omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.

Constraints:

• The number of nodes in the tree is in the range [1, 104]
• -1000 <= Node.val <= 1000

Python Solution

class Solution:
    def tree2str(self, root: Optional[TreeNode]) -> str:
        if not root:
            return ""
        
        result = str(root.val)
        
        if root.left or root.right:
            result += "(" + self.tree2str(root.left) + ")"
        
        if root.right:
            result += "(" + self.tree2str(root.right) + ")"
            
        return result

Java Solution

class Solution {
    public String tree2str(TreeNode root) {
        if (root == null) {
            return "";
        }
        
        StringBuilder result = new StringBuilder();
        result.append(root.val);
        
        if (root.left != null || root.right != null) {
            result.append("(").append(tree2str(root.left)).append(")");
        }
        
        if (root.right != null) {
            result.append("(").append(tree2str(root.right)).append(")");
        }
        
        return result.toString();
    }
}

C++ Solution

class Solution {
public:
    string tree2str(TreeNode* root) {
        if (!root) {
            return "";
        }
        
        string result = to_string(root->val);
        
        if (root->left || root->right) {
            result += "(" + tree2str(root->left) + ")";
        }
        
        if (root->right) {
            result += "(" + tree2str(root->right) + ")";
        }
        
        return result;
    }
};

JavaScript Solution

/**
 * @param {TreeNode} root
 * @return {string}
 */
var tree2str = function(root) {
    if (!root) {
        return "";
    }
    
    let result = root.val.toString();
    
    if (root.left || root.right) {
        result += "(" + tree2str(root.left) + ")";
    }
    
    if (root.right) {
        result += "(" + tree2str(root.right) + ")";
    }
    
    return result;
};

C# Solution

public class Solution {
    public string Tree2str(TreeNode root) {
        if (root == null) {
            return "";
        }
        
        StringBuilder result = new StringBuilder();
        result.Append(root.val);
        
        if (root.left != null || root.right != null) {
            result.Append("(").Append(Tree2str(root.left)).Append(")");
        }
        
        if (root.right != null) {
            result.Append("(").Append(Tree2str(root.right)).Append(")");
        }
        
        return result.ToString();
    }
}